\( \Large \displaystyle \frac{sinx}{x} \)の極限

\( \Large \displaystyle \frac{sin \ x}{x} \)の極限を考えていきます．

・マクローリン展開から

ここ，にあるように，正弦関数のマクローリン展開は，

\( \Large sin \ x = x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 + \cdots \)

\( \Large \simeq x \)

なので，

\( \Large \displaystyle \frac{sin \ x}{x} \simeq 1\)

となります．

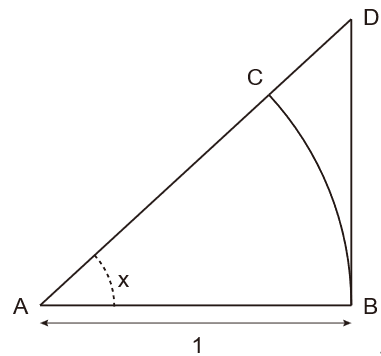
・面積から

こちら，を参考にしました．

図のように，0 < x < π/2，において，

\( \Large \displaystyle S_{ \Delta ABC} = \frac{1}{2} sin \ x\)

\( \Large \displaystyle S_{ fan ABC} = \frac{1}{2} x\)

\( \Large \displaystyle S_{ \Delta ABD} = \frac{1}{2} tan \ x\)

ここで，f(x) = tan x – xを考えます．

\( \Large \displaystyle f(x) =tan \ x - x = \frac{sin \ x}{cos \ x} - x\)

\( \Large \displaystyle f'(x) =tan \ x - x = \frac{cos \ x}{cos \ x} + \frac{sin^2 \ x}{cos^2 \ x}- 1 = \frac{sin^2 \ x}{cos^2 \ x} = ( tan \ x)^2 \)

タンジェント関数は上記の範囲で正の値なので，単調増加関数です．

x=0においては，

\( \Large \displaystyle f(0) =tan \ 0 - 0 = 0 \)

となるので，f(x)は，常に正の値となります，したがって，

\( \Large \displaystyle tan \ x - x \geq 0 \)

\( \Large \displaystyle tan \ x \geq x \)

となるので，

\( \Large \displaystyle \frac{1}{2} sin \ x \leq \frac{1}{2} x \leq \frac{1}{2} tan \ x \)

\( \Large \displaystyle sin \ x \leq x \leq tan \ x = \frac{sin \ x}{cos \ x} \)

sin x，で割ると，

\( \Large \displaystyle \frac{sin \ x}{sin \ x} \leq \frac{x}{sin \ x} \leq \frac{1}{cos \ x} \)

逆数ととると符号が逆転するので，

\( \Large \displaystyle cos \ x \leq \frac{sin \ x}{ x} \leq 1 \)

\( \Large \displaystyle \displaystyle \lim_{ x \to \infty }cos \ x = 1 \)

となるので，結果として，

\( \Large \displaystyle \displaystyle \lim_{ x \to \infty } \frac{ sin \ x}{x} = 1 \)

となります．